In my last blog post I wrote about the asymptotic equipartition principle. This week I will write about something completely unrelated.
This blog post evolved from a discussion with Brendan O'Connor about science and evidence. The back story is as follows. We were talking about Central Square (Cambridge, MA) and how it is sort of sketchy at night. Brendan mentioned that he had heard some stories about muggings in the area, and I said "Oh yeah, I heard about someone whose place got robbed recently." To which Brendan replied, "Was it in Central?" I told him that I didn't know but that it probably was.
We then got on the topic of whether a crime with an unknown location provided evidence for Central being sketchy. Brendan (who I later learned formalized confirmation bias for his master's thesis) wisely argued that it would depend on the model. I think this is a great point, so in this post I will examine two models that lead to differing conclusions.
I will consider a simplified situation in which there are two areas in town, C and K, and four crimes. The first two crimes occurred C, the third in K, and the fourth may have occurred in either C or K. I will present two alternative statistical models for estimating the "crimeyness" (Brendan's word) of C and K.
The first model treats each crime as an independent draw from a categorical distribution, i.e., each crime occurs in area C with probability (crimeyness) $p$ and in area K with probability $1 - p$. Letting $x_i$ be the location of the $i$th crime, the likelihood function is then
\begin{align*}
&P(x_1 = C, x_2 = C, x_3 = K, x_4 = C \lor x_4 = K \ |\ p)
\\&= P(x_1 = C, x_2 = C, x_3 = K, x_4 = C \ |\ p)
\\&\quad + P(x_1 = C, x_2 = C, x_3 = K, x_4 = K \ |\ p)
\\&= P(x_1 = C, x_2 = C, x_3 = K \ |\ p) ,
\end{align*}
which is just the likelihood of the data without counting the crime in the unobserved location. Thus in this case, that crime adds no evidence for the crimeyness of C.
Roger Grosse inspired the second model I examine here with his insightful comment that, really, the observation of a crime in an unknown location provides evidence for higher crimeyness in all areas.
This model assumes that the number of crimes in C, $n_C$, and the number of crimes in K, $n_K$, have independent Poisson distributions with rate (crimeyness) parameters $r_C$ and $r_K$, respectively.
Ignoring the fourth crime, the likelihood function would be
$P(n_C = 2, n_K = 1 \ |\ r_C, r_K) = P(n_C = 2 \ |\ r_C ) P(n_K = 1 \ |\ r_K),$
which looks like: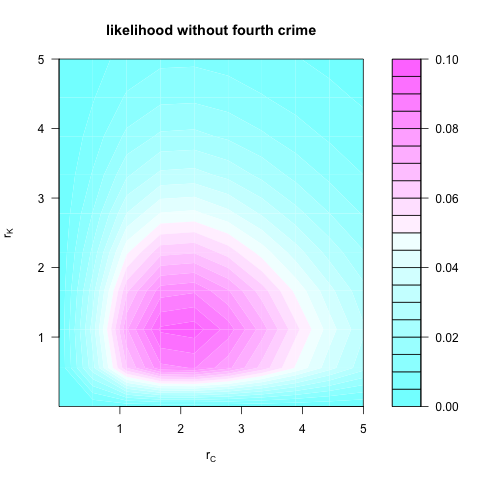
However, including the fourth crime gives the likelihood
\begin{align*}
&P(2 \leq n_C \leq 3, 1 \leq n_K \leq 2, n_C + n_K = 4 \ |\ r_C, r_K)
\\&= P(n_C = 3, n_K = 1 \ |\ r_C, r_K)
\\&\quad + P(n_C = 2, n_K = 2 \ |\ r_C, r_K)
\\&= P(n_C = 3 \ |\ r_C)P(n_K = 1 \ |\ r_K)
\\&\quad + P(n_C = 2 \ |\ r_C)P(n_K = 2 \ |\ r_K),
\end{align*}
which looks like: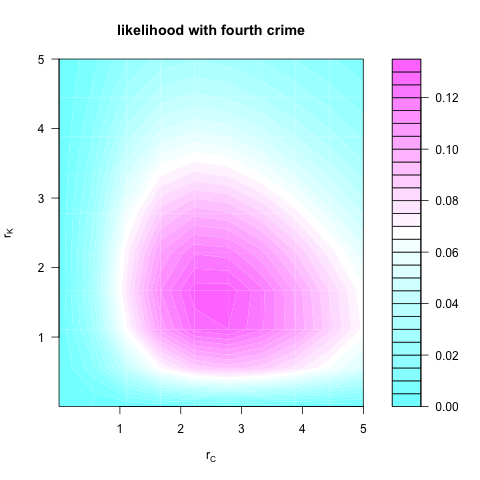
It is clear, then, that including the fourth crime in the second analysis increases the evidence for high crimeyness in both C and K. Thus, as Brendan suggested, whether the crime in the unknown location adds to the evidence of crimeyness depends on the model you use.
Moral of the story: Don't go to Central.
Homework: Is there a model under which the fourth crime provides evidence for higher crimeyness in C but not for higher crimeyness in K?
Also: R code for the plots
Free-association: citogenesis
Disclaimer: Please email me if you find any errors!
