Here's an interesting question: how much space would it take to store the genomes of everyone in the world? Well, there are about 3 billion base pairs in a genome, and at 2 bits per base (4 choices), we have 6 billion bits or about 750 MB (say we are only storing one copy of each chromosome). Multiply this by 7 billion people and we have about 4800 petabytes. Ouch! But we can do a lot better. We know that genomes of different humans are very similar; let's say 99.9% similar. For the calculations that follow I'll make the simplifying assumption that there exists some prototype genome, and that all other human genomes differ from it by exactly 0.1%, that is to say they differ from it at exactly 3 million locations. I will also assume that all allowed genomes are equally likely.
How do we use this assumption to compress genomes? First, consider the following simple scheme: we store the prototype genome, and then for each new genome, we store the locations of the changes, and the changes themselves. Since $2^{32}$ is about 4 billion, a regular 32 bit integer is enough to store the change locations. Then let's use an extra 2 bits to store the actual new base, for a total of 34 bits per change. With 3 million changes, this gives us a size of about 3 million $\times$ 34 bits = 13 MB per genome. That's already a lot better than 750 MB. But, can we do better? (Notation pit-stop: I will use the shorthand M for million and B for billion... but MB is still megabyte! I will use $\lg$ to mean log base 2.)
Luckily, Shannon figured out the theoretical limit on how much we can compress things. According to Shannon, since every allowed genome is assumed to be equally likely, all we need to do is count the number of allowed genomes and then take the log. The number of possible sets of change locations is $\binom{3B}{3M}$, or "3 Billion choose 3 Million", because we need to pick 3M change locations of out 3B possible locations. For each of these sets, we need to choose the new bases themselves, and there are 3 choices per base. So the total number of possible allowed genomes is \[\binom{3B}{3M} 3^{3M} = \frac{3B!}{3M! (3B-3M)!} 3^{3M}= \frac{3B!}{3M! 2.997B!} 3^{3M}\] Now, we take the log of this to get the minimum file size: \[\lg{3B!}-\lg{3M!}-\lg{2.997B!}+3M\lg{3}\]Using Stirling's formula, $\log{n!}\approx n\log{n}$, this gives us \[3B\lg{3B}-3M\lg{3M}-2.997B\lg{2.997B}+3M\lg{3}\](Note: I only kept the first term in Stirling's approximation. It turns out that the next term cancels out in this case, so I skipped it for the sake of cleanliness.) From here we can just compute the result with a normal calculator and we get about 39 million bits, or about 5 MB.
What does this mean? When we took advantage of the similarity of genomes, we compressed from 750 MB to 13 MB (about 90 PB for 7 billion people, down from 4800 PB). But the calculation above says that the theoretical limit is 5 MB. Why is our algorithm 8 MB shy of the optimum? In other words, from an intuitive point of view, where is the "slack" in our method? You might enjoy thinking about this for a minute before reading on.
I have identified 3 sources of slack in the above algorithm.
- We used 2 bits for every base change, but actually there are only 3 possibilities for a change, not 4. So, theoretically, we only need $\lg{3}\approx 1.6$ bits per change, instead of 2 bits.
- (a) We used 32 bits to store each change location (which is a number between 1 and 3 billion), but actually we only need $\lg(3B)\approx 31.5$ bits. (b) Furthermore, we don't even need this many $(\lg 3B)$ bits every time: the first time we need a number between 1 and 3B, but next time we only need to choose between 3B-1 locations, and then 3B-2, etc. since there are no repeats.
- The set of changes is sent in a particular order, which is irrelevant. We could permute the list of changes, and the resulting genome would be the same.
The next question is: what is the size of each of these effects? I will address these in the same order as they appear above.
- Using 2 bits instead of $\lg{3}$ bits per change has a total waste per genome of $3M\cdot (2-\lg{3})$ which is about 1.2 million bits or 0.15 MB.
- (a) Using 32 bits instead of $\lg{3B}\approx 31.5$ bits per change has a total waste per genome of $3M (32-\lg{3B})$, which is about 1.6 million bits or 0.19 MB.
(b) The size of effect 2(b) is the difference between sending $\lg{3B}$ bits 3 million times and the slightly more optimal version of sending $\lg{3B}$ bits, then $\lg{(3B-1)}$, and so on until $\lg{2.997B}$ bits for the last change location. Mathematically, this difference is \[(3M\cdot\lg{3B})-(\lg{3B}+\lg{(3B-1)}+ \ldots + \lg{2.997B})\]This effect is very tiny, only about 2000 bits or 0.00025 MB. - Sending an ordered list when ordering is not necessary means that all possible orderings of the 3M changes produce the same result. Since there are $3M!$ possible orderings of 3M changes, there is a redundancy factor of $3M!$ in this method. Thus the ordering has a waste of $\lg{3M!}$ bits. Here I again need Stirling's formula, and this time I will keep the second term because it does not cancel. Stirling's formula says\[\log{n!}\approx n\log{n}-n=n\log{(n/e)}\]We can again change this to log base 2 because the correction factor cancels from both sides, so we have\[\lg{3M!}\approx 3M\lg{(3M/e)}\]which is about 60 million bits or 7.5 MB.
Let's take a moment to interpret these results. First, it's interesting that almost all of the slack comes from the ordering issue, slack source #3. This was not very intuitive to me at first; it seems like such an abstract concept that "we send things in some particular order but actually the order doesn't matter", but this "abstract" concept costs us 7.5 MB, or about 52 petabytes for all 7 billion genomes. Hopefully this issue will become more clear in the following paragraphs.
Second, did we find all of the slack? The original algorithm was 13 MB (actually 12.75 MB) and the theoretical limit was 5 MB (actually 4.87 MB). We found a total of 0.15 MB + 0.19 MB + 0.00025 MB + 7.53 MB = 7.87 MB of slack. Add this to the theoretical limit of 4.87 MB and we get 12.74 MB. This seems plausibly within rounding error of 12.75 MB, which is great! But, maybe we still missed something?
The answer is that we did not miss anything. Below, I will show definitively that we found all the slack. In particular, I will show how, starting with the mathematical expression for the theoretical minimum, $\lg{3B!}-\lg{3M!}-\lg{2.997B!}+3M\lg{3}$ bits, we can act on it with each slack source in turn and end up with the exact mathematical expression for our algorithm, $3M\cdot32 + 3M\cdot2$ bits. Here we go... [it is possible to skip the next 3 paragraphs if you believe me and do not need to see the calculations]
First, we apply slack source 1, which connects the $3M\lg{3}$ term to the $3M\cdot 2$ term. Slack source 1 says that there are only 3 choices for a change of base, not 4. This corresponds exactly to changing the $\lg{3}$ to $\lg{4}=2$ for each change, or $3M\lg{3}$ to $3M\lg{4}=3M\cdot 2$ bits in total.
Next we apply slack source 2, which connects $\lg\frac{3B!}{2.997B!}$ to $3M\cdot 32$. We start with slack source 2(b). In the theoretical calculation we started with the ratio $\frac{3B!}{2.997B!}$, which is the same as $3B\times (3B-1)\times ... \times 2.997B$. This product is fairly similar to $3B\times 3B\times ... \times 3B$, or $(3B)^{3M}$. Indeed, the mathematical approximation $\frac{3B!}{2.997B!}\approx3B^{3M}$ exactly corresponds to slack 2(b): it is the intuitive approximation that it is OK to just send $\lg{3B}$ bits per change location, instead of the slightly optimized version described above. Then, from there, $\lg{(3B)^{3M}}=3M\lg{3B}$, and effect 2(a) above says that we approximate $\lg{3B}$ as 32. When we apply this approximation, we get $3M\cdot 32$, which is exactly the term we were looking for.
Finally, we apply slack source 3. The only term left in the theoretical formula is the $3M!$ in the denominator, which has no corresponding term in the formula for our algorithm. This is exactly slack source 3, as described earlier! The slack due to ordering has a redundancy of $3M!$ possible orderings, and when we divide this out in the "choose" formula, this exactly corresponds to saying that, in theory, we do not need ordering, so we divide these permutations out, thus reducing the theoretical limit by exactly $\lg{(3M!)}$ bits.
To recap: I have now shown that the formula for the size of our algorithm can be obtained by starting with the theoretical formula and applying a series of mathematical approximations, and furthermore that each of these approximations exactly corresponds to one of the intuitive slack sources described above. Thus, we have "found" all the slack; i.e. we have an intuitive understanding of all the reasons why our method for storing genomes compresses less than the theoretical limit.
I want to add one last chapter to the story, namely to address the obvious question: "What is a better algorithm that performs closer to the theoretical limit?" One intuitive answer is the following: instead of encoding the change locations explicitly, encode the distances ("diffs") between subsequent change locations. For example, instead of transmitting that there are changes at locations 195, 200, and 240, just encode "195", "5", and "40". Intuitively, these diffs will be small, on average 1000 or so. By transmitting smaller numbers, we can save bits. Using our newfound intuition, we can also say definitively that encoding the diffs eliminates the order-based slack, because the diffs must be sent in the proper order for the answer to be correct. [Note: the discussion below about diffs is meant to illustrate the intuitions described above, and is not necessarily the best solution. To solve this problem more optimally, I would probably use arithmetic coding. A new method for compressing unordered sequences is described in this paper.]
To make this more concrete, I propose the following algorithm: sort the locations of all the changes and find the diffs. Then, use $n<32$ bits to encode each diff. If a particular diff requires more than $n$ bits (i.e., is $\geq 2^n$), then we will send a special symbol of $n$ zeros, followed by the full 32-bit representation of the diff. How do we choose $n$? Intuitively, if we pick $n$ too small then almost all of the diffs will overflow and we will end up sending them as full 32-bit representations, gaining nothing. On the other hand, if $n$ is too large then we don't get significant gains because the diffs are sent with more bits than needed. Thus we can expect some middle ground that gives the best performance.
To test this, I implemented a codec using this method. I first generated random genomes using the assumptions above, then compressed them with this method and plotted the performance as a function of $n$. The results are shown in the figure below. (Code is posted here.)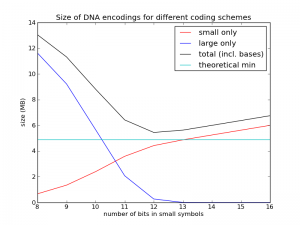
The cyan line is the theoretical limit, at about 4.9 MB. The red line shows just the size of the diffs represented with $n$ bits. The blue line shows just the size of the diffs represented with $n+32$ bits (the "overflows"). The black line is the sum of the red line, the blue line, and the $3M\cdot 2$ bits used for the new bases (as you can see, I didn't bother addressing slack source 1, but at least now I know it only costs me 0.15 MB per genome). What we see is just what we expected: things get worse, and then they get better. In this case we see the best value is $n=12$, and its size is about 5.4 MB, quite close to the theoretical limit.
To improve a diff-based system further, one would have to take into account the probability distribution of the diffs. Below is an empirical histogram of this distribution from one random genome I generated. (Quick sanity check: the picture is approximately a triangle with base length 2000 and height 0.001, so its area is plausibly equal to 1). Intuitively, the algorithm above is optimal for a distribution that is different from this one. In particular, the algorithm "thinks" the distribution is a piece-wise constant function with two pieces, one higher-probability piece between 1 and $2^n-1$ and another, lower-probability piece from $2^n$ to 3B. Changing $n$ changes the shapes of these steps, and presumably choosing $n=12$ maximizes the "overlap" between the implied piece-wise distribution and the real distribution (approximately) shown here.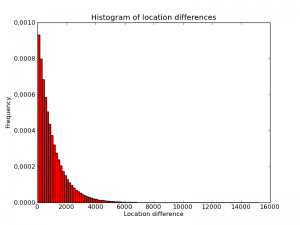
Comments, questions, or corrections? Please email me! My email is listed near the top of my website.
