As the title of the post suggests, this week I will discuss a geometric intuition for Markov's inequality, which for a nonnegative random variable, $X$, states
$$
P(X \geq a) \leq E[X]/a.
$$
This is a simple result in basic probability that still felt surprising every time I used it... until very recently. (Warning: Basic measure theoretic probability lies ahead. These notes look like they provide sufficient background if this post is confusing and you are sufficiently motivated!)
I used to get intuition for Markov's inequality from the fairly intuitive proof (or the equivalent proof with integrals),
\begin{align*}
E[X] &= \sum_x x P(x)
\\
&= \sum_{x < a} x P(x) + \sum_{x \geq a} x P(x)
\\
&\geq \sum_{x \geq a} x P(x)
\\
&\geq \sum_{x \geq a} a P(x)
\\
&= a\sum_{x \geq a} P(x)
\\
&= a P(x \geq a),
\end{align*}
which is all well and good, but I like pictures and don't feel like I have really internalized a concept unless I have a representative picture for it in my mind. The problem is then, what is the picture here? Expectations are averages, so when you look at the value of $E[X]$ it is kind of at the center of the distribution, but how is that related to the probability in the tail of the distribution?
This might be overkill, but in my mind, the key to an intuitive geometric understanding of Markov's inequality relies on a measure theoretic view of probability. What measure theoretic probability gives us in this case is a geometric perspective of expectations, from which Markov's inequality falls out immediately.
Recall that random variables are actually functions. A random variable is defined with respect to a probability triple, $(\Omega, \mathcal{F}, P)$. The function $X\colon \Omega \rightarrow \mathbb{R}$ is a random variable if it is a measurable function in the sense that the preimage $X^{-1}(A) = \{\omega \in \Omega\ |\ X(\omega) \in A\}$ is always measurable, so we can write $P(X \in A) = P(\omega \in X^{-1}(A))$.
The key is then that $E[X]$ is essentially just the area under the random variable $X$ since $E[X] = \int_\omega X(\omega) dP $. We can then understand Markov's inequality from the following (slightly simplified) picture: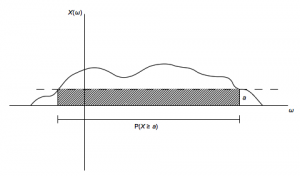
The dashed line is at the height $a$, so the probability that $X$ is greater than $a$ in this case is just the length of the contiguous set of values $\omega$ that map to values of $X(\omega)$ greater than $a$ (the line segment shown in the picture). The area of the shaded box is thus $a P(X \geq a)$, which is clearly less than the entire area under $X(\omega)$. Hence $a P(X \geq a) \leq E[X]$ as desired.
