When we talk about priors and regularization, we often motivate them in terms of "incorporating knowledge" or "preventing overfitting." In a sense, the two are equivalent: any prior or regularizer must favor certain explanations relative to others, so favoring one explanation is equivalent to punishing others. But I'll argue that these are two very different phenomena, and it's useful to know which one is going on.
The first lecture of every machine learning class has to include a cartoon like the following to explain overfitting: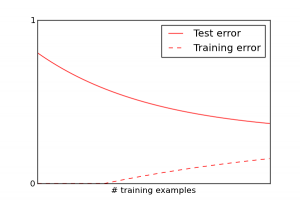
This is more or less what happens if you are using a good and well-tuned learning algorithm. Algorithms can have particular pathologies that completely distort this picture, though.
Consider the example of linear regression without a regularization term. I generated synthetic data with $D = 100$ feature dimensions, with everything drawn from Gaussian priors. Recall that the solution is given by the pseudoinverse formula $X^\dagger y$, i.e. from the set of points which minimize error on the training set, it chooses the one with the smallest norm. Here's what actually happens to the training and test error as a function of the number of training examples $N$ (the dotted line shows Bayes error):
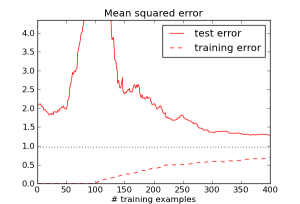
Weird -- the test error actually increases until $N$ roughly equals $D$. What's going on?
When $N \ll D$, it's really easy to match all the training examples. E.g., when N = 1, there's a $D-1$ dimensional affine space which does this. But as $N$ becomes closer to $D$, it gets much harder to match the training examples, and the algorithm goes crazy trying to do it. We can see this by looking at the norm of the weight vector $w$:
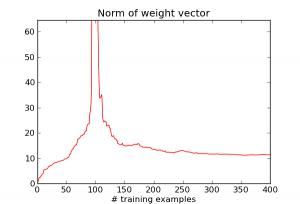
So really, the large error is caused by the algorithm doing something silly: choosing a really large weight vector in order to match every training example. Now let's see what happens when we add an L2 regularization term $\lambda \|w\|^2$. Here are the results for several different choices of lambda:
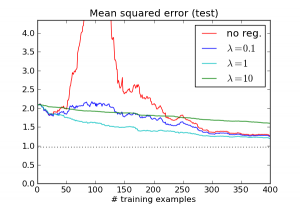
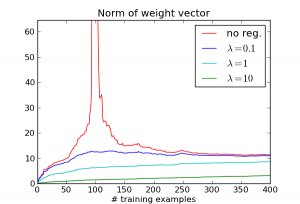
The effect disappears! While the different $\lambda$ values occupy different points on the overfitting/underfitting tradeoff curve, they all address the basic issue: the regression algorithm no longer compulsively tries to match every example.
You might ask, doesn't this regularizer encode information about the solution, namely that it is likely to be near zero? To see that the regularization term really isn't about this kind of knowledge, let's concoct a regularizer based on misinformation. Specifically, we'll use an L2 regularization term just as before, but instead of centering it at zero, let's center it at $-w$, the exact opposite of the correct weight vector! Here's what happens:
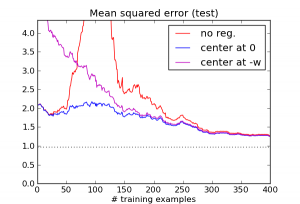
This is indeed a lousy regularizer, and for small training set sizes, it does worse than having no regularizer at all. But notice that it's still enough to eliminate the pathology around $N=D$, and it continues to outperform the unregularized version after that point.
Based on this, I would argue that for linear regression, L2 regularization isn't encoding knowledge about where good solutions are likely to be found. It's encoding knowledge about how the algorithm tends to misbehave when left to its own devices.
Usually, priors and regularizers are motivated by what they encourage rather than what they prevent, i.e. they "encourage smoothness" or "encourage sparsity." One interesting exception is Hinton et al.'s paper which introduced the dropout trick. Consider the title: "Improving neural networks by preventing co-adaptation of feature detectors." Co-adaptation refers to a situation where two units representing highly correlated features wind up with opposing weights. Their contributions wind up mostly canceling, but the difference may still help the network fit the training set better. This situation is unstable, because the pair of units can wind up behaving very differently if the data distribution changes slightly. The dropout trick is to randomly turn off 50% of the units on any given iteration. This prevents co-adaptation from happening by making it impossible for any two units to reliably communicate opposite signals.
Next time you try to design a prior or regularizer, think about which you're doing: are you trying to incorporate prior knowledge about the solution, or are you trying to correct for the algorithm's pathologies?
